The Jumbo Jet Illusion: Why are They so Slow?

Marc Green

You see a jumbo jet plane flying across the sky. Consciously, you know that it is flying many hundreds of miles per hour, yet it seems to crawl at a barely perceptible speed. What causes the disparity between perception and knowledge? The question has several answers, but the most important is that humans are not well-designed to perceive depth.

1. Misjudged Depth

As explained elsewhere, the 3-D world projects an image on to the retina, which is only 2-D. There is no direct representation of depth so distance along the Z-axis is completely lost. The result is the "inverse projection problem." Given a 3-D world, it is possible to specify its image projection onto a 2-D surface, such as the retina. Given a 2-D image, on the other hand, it is impossible to specify the world that created the projection. An infinite number of 3-D worlds could have produced any given retinal image.

The lack of retinal depth information potentially has far-ranging implications for perception. Most notably, a viewer cannot judge the distance of objects. Less obviously, a viewer who cannot judge depth also cannot judge shape, size or speed. Figure 1 shows how depth, size, and speed are all interconnected in judging the speed of a jumbo jet flying overhead.


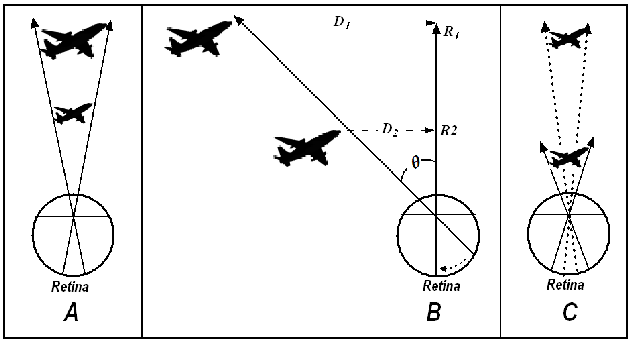
Figure 1 The relationship among depth, size, and speed is evident in the jumbo jet's slow movement.

Panel A depicts the retinal image created by a jet viewed at different distances. An infinite number of size-distance combinations could have produced any given sized retinal image. Panel A demonstrates that the same sized retinal image of an airplane could be due to a large plane far away or to a small plane nearby. Panel C shows the inverse problem that two objects of the same physical size create very different sized retinal images at different distances. The result is a catch-22. The viewer needs to correctly perceive distance to correctly perceive size, and the viewer needs to correctly perceive size to correctly perceive distance.

Panel B shows why depth information is needed for accurate speed perception. A jumbo jet moving in tangential motion across the sky seems to travel at a snail's pace. Even the conscious knowledge that it is traveling at many hundreds of miles per hour does not alter the illusion, demonstrating its "cognitive impenetrability." It is not open to introspection. Assume that the jet moves across the sky at range R1 in the depth plane. A viewer watching the jet for a period of time sees it move rightward across a given visual angle of space. For this to occur, the jet must have moved a distance D1 in space during the time T that the viewer watched. The viewer can theoretically infer the jet's speed if distance and time are known because speed (velocity) is distance/time, i.e.:

V=D/T

The inference about speed depends on correctly perceiving the jet's distance in depth. Suppose the jet were physically closer at range R2. In this case, the jet moved only distance D2, much less than D1 in the same time interval. Since it covers a shorter distance, it must then be moving at a slower speed,

In sum, the closer the jet appears relative to its physical distance, the slower it appears to travel. Note that the viewer cannot use the jet's size to judge distance because, as Panel A shows, the retinal image alone could represent a jet at any distance. Viewers underestimate the distance and are unable to reconstruct 3-D space accurately.

The observant reader may have noted that if the viewer judged speed from the change in the optical angle with the eye over time (angular velocity Θ/T degrees/second) then no 3-D reconstruction would be necessary because Θ is independent of depth. The reason that humans do not use angular velocity is that the system that directly detects angular velocity is relatively insensitive to slow motion. See below.

This still leaves the question as to why the jet's distance is underestimated. One factor is size. Jets are very large objects, so they create a relatively large retinal image regardless of distance. Large retinal images indicate nearby objects. If this is true, then an object's speed should seem faster if its size is underestimated and hence distance overestimated. Hershenson & Samuels (1999) described just this effect when an observer mistook a drone for a full size airplane and judged its speed to be abnormally fast. Both the drone's small retinal image size and its familiar size cue caused the perception of great distance. Hence it must have been moving very fast.

However, the most important factor is likely the compression of apparent visual space with range. Perceived depth (distance along the Z-axis) is a "compressive function" that follows Stevens's Law:



Perceived sensation is a power function of physical intensity, with the exponent of a. (k is a linear scaling constant that varies with the context.) The important point is that when a is below one, the resulting function is "compressive," it grows at an increasingly lower rate as sensation increases. The result is a graph looks something like Figure 2.


Figure 2 Stevens's Law for a compressive function. Note that perceived intensity grows at an increasingly lower rate as physical intensity increases.

With a compressive function, perceived quantity does not increase as fast as the physical quantity. For example, a light with twice the intensity of another appears less than twice as bright. Similar compression occurs in depth, although the exact exponent (a) varies across studies. The compressive effect is greater with increasing distance. In far space of a kilometer or more, the exponent is as low as about 0.4, indicating very great compression (e.g., Flückiger, 1991). Viewers then drastically underestimate the range and speed of distant objects, such as jumbo jets.

The compression of depth is also shown in studies that compare apparent distance in depth (Z) with distance along the frontoparallel plane (X/Y), which cuts a right angle across the sightline. When asked to set the distances equal, viewers set the depth (Z) distance 50-90 percent as great as X or Y distance (Loomis, Da Silva, Fujita, & Fukusima, 1992). This is to be expected as the exponent for frontoparallel plane distance is higher and often about one. Unlike distance in the Z plane, distances in the X (and Y) plane are represented on the retina. However, translating that X/Y plane retinal motion into a perceived object motion still requires recovery of depth.

2. Absence of Stationary References

Other factors also contribute to the illusion. The jet hangs in a featureless sky, which has two effects. First, there are no other depth cues, which impairs distance estimation (e.g., Holway & Boring, 1941). When present, depth cues that change perceived distance can drastically alter perceived speed (Gillen, 2017). Second, perception of slow to moderate speed is object-relative, depending on the change in position between the moving object and stationary background. In one of the classic perception studies (Brown, 1931) found that objects appear to move much more slowly in an open field than when a frame or stationary marks are present. The relatively empty sky offers few stationary objects for perceiving the relative motion. Everyone has probably noticed that clouds appear to move faster when passing behind trees or buildings, which serve as stationary references. The jet will appear faster if there are cloud contours behind it.

However, object-relativity is only important for slow retinal motions because they are inferred from change in position. The visual system has at least two motion processing mechanisms (e.g., Green, Chilcoat, and Stromeyer, 1981). The one that infers motion from position is likely mediated by the focal/ventral/pravocellular part of the brain that registers objects and their locations. The ambient/dorsal/magnocellular part of the brain directly senses motion and is most sensitive at higher velocity. As explained in the discussion of rear-end collisions, driver judge closing rate using the indirect system at long distance when retinal image motion is slower and the direct system only at short distances when retinal image motion is faster.

3. Intuitive Physics

Another possible contributing factor is the misperception of physics. Most people are not physicists, so their commonsense understanding of the material world is based on an informal "naive" or "intuitive" physics (e.g. McCloskey, 1983). This understanding is often incorrect. One example is that heavier objects appear to move slower, presumably because it takes more force to get them moving (e.g., Bitoh, 1991; Hubbard, 1997). A pushed refrigerator moves slower than the pushed cardboard box that it came in. Jumbo jets are very heavy, so they intuitively move slower. (Movies and computer graphics take advantage of this by making large objects such as monsters, etc. appear to move very slowly to show their size.) Another example of an intuitive physics error is "representational momentum." Viewers judge the stopping location of a motion beyond its actual point of rest as if a momentum continued to carry it along its trajectory.

4. Lack of Ground Contact.

Most theories of visual space perception are "air theories" which assume that the spatial locations of objects is defined by the objects themselves. Gibson (1950) objected to this idea by noting that the distance to an object is filled with empty space. We perceive through space/air but we do not perceive the space/air itself. Gibson is famous for saying that "Space is a myth, a ghost, a fiction for geometers."

Instead, he proposed a "ground theory" of perception where the object location is defined by its position on the ground plane, the surface that runs from the viewer's feet to the horizon. (Here "horizon," is defined as the endpoint of the ground plane, not necessarily the point where the sky meets the ground.) Airplanes hang in the sky with no contact on the ground plane so their distance is inherently ambiguous. Some research has confirmed Gibson's view that ground plane position is important in judging depth.

The Jumbo Jet Illusion on the Ground?

Interestingly, the jumbo jet illusion does not seem to occur strongly under other, superficially similar circumstances. A driver traveling down the road may see a pedestrian or another vehicle moving across his path, much as the jet moves across the sky. A comparison between the jet ground observer and the car driver scenarios is instructive since it highlights the importance of the Z-axis depth dimension. Unlike the ground observer, the driver does not drastically underestimate the speed, even if the object is several blocks away. Instead, the pedestrian or vehicle seems to travel at a normal speed. Viewers can overcome the limitation of the 2-D retina and perceive depth to a degree of accuracy sufficient for more veridical speed judgments. The jumbo jet factors are reduced-the shorter depth has lower compression, stationary references help judgment of motion, visual cues aid depth judgments, and the object is on the ground plane.

Even on the roadway, however, speed judgments are prone to some degree of the jumbo jet illusion. For example, the jumbo jet illusion is often cited for causing grade crossing collisions. Trains are very large and drivers underestimate their speeds when deciding whether it is safe to cross the tracks (e.g., Clark, Perrone, & Isler, 2013).

Conclusion

In sum, the jumbo jet illusion occurs primarily due to a misjudgment of distance created by the compressive nature of visual space perception. It is magnified by the jet's large size, lack of stationary references, absence of ground contact, and possibly by faulty intuitive physics.

Lastly, the above discussion examined only one of two jumbo jet illusions. There is a complementary illusion where the person sitting in the jumbo jet looks through a window down at the scene below. Like the ground observer, he perceives the plane as crawling along despite knowledge of its high, actual speed. This has a very different explanation based on a another perceptual factor, the "GOFR." It is a story for another time.

---

A division of 2057949 Ontario, Inc.
Copyright © 2024 Marc Green, Ph. D.
Home Page
Contact Us