Why Drivers Say "He came out of nowhere"

Marc Green

The page A Crash Course in Collisions explained how geometry is a key aspect of collision analysis. Here, I expand the discussion to show how geometry produces a common collision phenomenon - the driver only sees the object that he has struck in the moment before impact. A common refrain is, "He came out of nowhere!"

Recall that in CBDR geometries, objects on collision course maintain a constant bearing angle so long as speed and direction are constant. However, the driver's eye is not on the front bumper, but typically back 6-8 feet (except in vans). This has consequences that become apparent when graphing the angles between the driver's eye and approaching object with decreasing TTC. Three angles are critical:

1. Front bumper. Bearing angle from the driver's front bumper to the approaching object.

2. Retinal eccentricity. Because the driver's eye is 6-8 feet back, bumper and eye bearing angles are different. If the bumper is on a CBDR, then the eye is not. The bearing angle with respect to the driver's eye is the "retinal eccentricity", which gives the object's angular distance from the fovea. An object with a retinal eccentricity of 10 degrees, for example, forms an image 10 degrees from the fovea in peripheral vision. The object is more difficult to see because it is: 1) farther from the center of attention, 2) in a retinal area of lower contrast sensitivity, 3) more subject to crowding effects, and 4) more likely hidden behind a sightline obstruction.

3. Headlamp beam aim. The bearing angle of the object with respect to the headlamp beam differs from the front bumper. Headlamps aim to the right (and down).

Bearing and Visual Angles

The difference between bearing angle and retinal eccentricity depends on distance, or equivalently, time-to-collision (TTC). Assume that a pedestrian is crossing the road at 5 ft/sec from left to right in front of a driver traveling at 30 mph. Figure 1 shows the critical angles.


Figure 1 Angles as TTC shrinks. The vehicle is traveling at 30 mph, the pedestrian is walking at five ft/sec, and the driver's eye is seven feet from the front bumper.

Bearing Angle (pedestrian angle to front bumper). The dotted line shows the bearing angle between the front bumper and the pedestrian. As already explained, this is a CBDR so the bearing angle remains constant. Here it is 6.5 degrees, but the absolute value depends on the relative speeds of the vehicles and the crossing object. A jogger, bicycle (see below) or motorized vehicle would have a greater bearing angle.

Retinal Eccentricity (retinal image location): More importantly, the retinal eccentricity is not quite constant. Initially, the retinal eccentricity is about the same as the bearing angle, so the pedestrian forms an image at about 6.5 degrees in peripheral vision. As the time passes, the vehicle's bearing angle remains constant, so there is little retinal slip to draw attention. However, the retinal eccentricity begins to decrease very gradually until just before impact. Then it dramatically falls to zero, so in about the last half second the pedestrian moves from peripheral vision to right in the sightline.

Retinal Image Size & Looming rate. The size of the image projected on the retinal is quantified as the visual angle (roughly size/distance). As the driver comes closer, the pedestrian's retinal image size grows exponentially. This makes the pedestrian more visible and creates strong looming (retinal image size/rate of growth), the impression that a collision will occur. Again, there is a dramatic change within the last half-second or so, just before collision.

Higher object speed increases the bearing angle. In the example above, the bearing angle was small because pedestrians move relatively slowly, although a running pedestrian would create a larger angle. However, changes in the speed have little effect on the location of the asymptote and the basic fact that visibility factors all suddenly improve dramatically in about the last second or less prior to collision. Suppose that instead of a pedestrian, the collision is with a bicyclist moving 18 mph, which is a good but not abnormally high speed. Figure 2 shows that the results are similar to those in Figure 1, except that the bearing angles are much greater, meaning that the bicyclist is initially much farther in peripheral vision, specifically at 31 degrees. The retinal eccentricity again changes slowly until TTC is under a second. The change in eccentricity also creates image movement across the retina. The retinal slip is more dramatic for the bicycle than for the pedestrian because retinal eccentricity change is greater. This high retinal slip velocity provides a motion cue which may also draw driver attention at the very last moment.


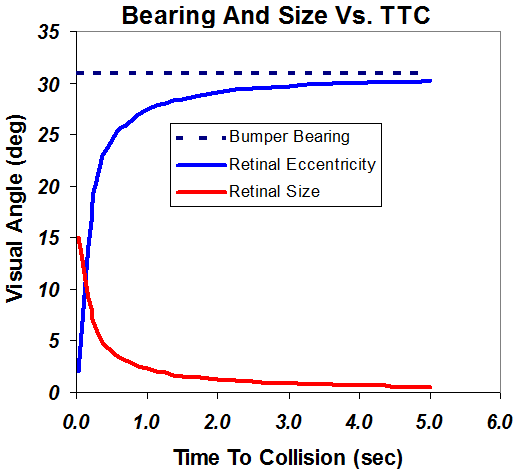
Figure 2 Angles as TTC shrinks. The vehicle is traveling at 30 mph, the bicycle is traveling at 18 mph, and the driver's eye is seven feet from the front bumper.

Illumination

If the collision occurs at night, then headlamp illumination angle is another factor. Headlamps have a beam-spread function, meaning that they are strongest in the center and become weaker as the angle departs from the aiming direction. At a longer TTC, moreover, the pedestrian is farther away and receives less illumination.

Headlamp strength is measured as luminous intensity in units of candela (cd). A typical intensity is 22740 cd at the center, which aims 1R,1D, meaning one degree rightward and one degree downward from straight ahead. However, the beam is much weaker as the angle departs from the optimum. Headlamps throw 884 cd at an angle of 6.5L,0 and 4347 cd at 6.5L,1D.

Pedestrian illumination is a function of distance/TTC because illumination cd/distance². At constant velocity, distance varies linearly with TTC so illumination cd/TTC². Figure 3 shows how pedestrian illumination changes with TTC.

Illumination follows a similar trend as bearing angle and retinal size: it starts out low and changes only gradually until the last second when it suddenly lights up the pedestrian, even if he is wearing dark clothing. The curves' asymptotes don't depend too much on absolute headlamp intensity.


Figure 3 Illumination as a function of TTC.

For illumination, the drastic, last moment visibility change is not due to the (horizontal) bearing angle but rather to another nonlinear relationship: the Inverse Square Law. Illumination changes as the square of the distance. At 6.5L,1D, the same pedestrian who has 382 lux of illumination at TTC=0.25 drops to 95 lux at TTC=0.5 second because doubling the TTC/distance decreases illumination by a factor of four. Similarly, the illumination is only 6 lux at TTC=2.0 seconds (i.e., 95/4²). At 6.5L,0, the numbers are 78 lux at TTC=0.25 and 1! lux at TTC=2.0.

Moreover, the change in illumination with TTC is even greater because the analysis did not take vertical angle into account. Headlamp beams are very weak about the vertical in order to prevent glare. At TTC=2 sec the headlamp aims directly at the roadway and the pedestrian is getting the relatively weak upper portion of the headlamp beam. At TTC=0.25, the stronger beam center illuminates the pedestrian legs. For complete calculations, see Green (2017).

A plot of bicyclist illumination would look very much like Figure 2, except that the bigger bearing angle makes initial illumination much lower. The headlamp output is only about 101 cd at 31L,0 and 153 cd at 31L,1D. The bicyclist receives negligible headlamp illumination until he is very close to collision. Again, illumination would increase drastically at the last second or less as the bearing angle collapses toward zero.

The scenarios described above have used some simplifications which do not affect any conclusions. First, the collision is the left front bumper. The scenario changes slightly if the point of contact is on the vehicle's side or on the center/right front bumper. If impact is on the side, neither the bearing rate nor the retinal eccentricity ever reaches zero - in fact it grows as TTC decreases. If the point of impact is on the center/right front, then the bearing angle and retinal eccentricity reach zero a second or less before the collision. Neither of these factors substantially changes the situation. Second, I haven't bothered to correct for the driver's lateral position and put his eye at the vehicle's left edge, instead of about 1-1.5 feet from the door. This simplification also makes no significant difference.

Conclusion

It is hardly surprising that drivers often say that they didn't see the approaching object until the last moment. The explanation in many or most cases lies in simple geometry and photometrics, which change in a highly nonlinear way with distance/TTC. Critical visibility factors of 1) retinal eccentricity, 2) retinal size and slip velocity, and 3) illumination all remain relatively constant until about a second before collision. Whether the driver attempts to respond at all prior to the collision is problematic, but in most cases it doesn't matter because there is insufficient time for avoidance given the needed perception-response time, brake pedal depression and physical stopping distance.

A driver who has a collision is often blamed for "not looking where he was going." In most lateral collisions, exactly the opposite is true. Drivers generally look straight ahead toward the focus of expansion in the optic flow field, toward the rear of a lead vehicle or toward the end of their headlamp pools at night. Factors that increase driving difficulty, e.g., rain, fog, heavy traffic, bad road surface, etc., further reinforce and narrow the view straight ahead and compound the influence of geometry and the Inverse Square Law.

Footnotes

¹The headlamp data are taken from Schoettle, Sivak, Flannigan, & Kosmatka (2004). Instead of actually calculating the headlamp bearing angle, I just used a set of data that has the headlamp beam spread with respect to space, which is simpler when the needed data exist.

---

A division of 2057949 Ontario, Inc.
Copyright © 2024 Marc Green, Ph. D.
Home Page
Contact Us